C++で1次元ポアソン方程式を解く

理論

シンプルなタイトルですが，やってることもシンプルです．まずは1次元ポアソン方程式を見てみましょう．
$\frac{d^2V}{dx^2} = -\frac{\rho}{\eps}$
ここでVはポテンシャル，xは位置，ρは電荷密度，εは誘電率です．式を見ると微分が含まれていますね．コンピュータで微分を解くためには種々の方法がありますが，一番簡単なのは「差分法」ではないかと思います．コンピュータ上ではデータは離散的なので，ポテンシャルVをΔxでN個に分割したことを想定してください．1階微分は次のように前方差分と後方差分と呼ばれる連続する離散データの差で表すことが出来ます．
$\frac{\Delta V_+}{\Delta x} = \frac{V_{n+1} - V_{n}}{\Delta x}$
$\frac{\Delta V_-}{\Delta x} = \frac{V_{n} - V_{n-1}}{\Delta x}$
この前方差分と後方差分を使って2階微分は次のように表されます．
$\frac{d^2V}{dx^2} \simeq \frac{\frac{\Delta V_+}{\Delta x} - \frac{\Delta V_-}{\Delta x}}{\Delta x} = \frac{V_{n+1} + V_{n-1} - 2 V_n}{\Delta x^2}$
そして，最初の式と併せて $V_n$ について解くと，
$V_n = \frac{V_{n+1} + V_{n-1}}{2} + \frac{\rho}{\eps} \Delta x^2$
と得ることが出来ます．つまり，ある地点のポテンシャル $V_n$ は前後の領域のポテンシャル（とその地点の電荷密度）を用いて表すことが出来る訳です．
ここで，両端のポテンシャルを決めた場合を考えます．つまり1番目のポテンシャルとN番目のポテンシャルを確定させます．これはディリクレの境界条件と呼ばれます（電界＝-1階微分はノイマン）．2〜N-1は適当に数値を入れておきます．2番目のポテンシャルは1番目と3番目のポテンシャルを使って，3番目のポテンシャルはその結果求められた2番目のポテンシャルと4番目のポテンシャルを使って，4番目の…，とN-1番目まで計算します．これを繰り返し計算していくと段々と値が収束し，所望のポテンシャルが得られる，という寸法となります．
なお，この計算において逐次過緩和（SOR）法を用いると計算が高速化します．
$V_n = V_n + \omega \left( \frac{V_{n+1} + V_{n-1}}{2} + \frac{\rho}{\eps} \Delta x^2 - V_n \right)$
ここでω=1〜2とします．1の場合は完全に前の式と一致します．どの値が良いか，といったことは経験的に出すしかなく，私は1.8くらいを良く使います．

プログラム

では，このポアソン方程式を解くソースコードを以下に示します．
Poisson.h

#include <vector>
#include <iostream>
#include <cmath>

/*
@brief 1次元ポアソン方程式をSOR法により計算する（ディリクレ条件）
@param[out] V 対称のポテンシャルベクトル
@param[in]  x 対応する位置のベクトル
@param[in]  RhoOverEPS 電荷分布を表すファンクタ
@param[in]  minErr 収束最小値
@param[in]  maxStep 最大計算ループ数
@param[in]  w SOR法係数
*/
template <class Container, class Functor>
int solvePoisson1D(Container &V, const Container &x, Functor RhoOverEps,
				   const double minErr = 1e-6, const double maxStep = 1000, const double w = 1.9)
{
	using namespace std;

	// vectorサイズ一致の確認
	const int div = x.size();
	if (V.size() != div) {
		cout << "V.size() != x.size() @solvePoisson1D" << endl;
		return false;
	}

	// vector最小数
	if (div < 3) {
		cout << "V.size() < 3 @solvePoisson1D" << endl;
		return false;
	}

	// 単調増加か
	for (int i=0; i<div-1; i++) {
		if (x[i] > x[i+1]) {
			std::cout << "Error! x must be monotonically increasing. (@solvePoisson1D)" << std::endl;
			return false;
		}
	}

	// 微分幅を得る
	const double dx = x[1] - x[0];

	// 誤差初期値
	double err = 2*minErr;

	// ループ回数
	int step = 0;

	// 誤差が最小誤差よりも小さくなるか，maxStepに到達するまでセルフコンシステント計算
	double Vmax = 0.0;
	while (err > minErr && step++ < maxStep) {
		err = 0;
		// 差分法を適用
		for (int i=1; i < div-1; i++) {
			double Vp = V[i];

			// Poisson方程式
			V[i] = Vp + w * ( (V[i+1] + V[i-1])/2 + RhoOverEps(x[i])/2*dx*dx - Vp);

			// 規格化用Vを計算
			if (fabs(V[i]) > Vmax) {
				Vmax = fabs(V[i]);
			}

			// 誤差計算
			double dif = abs(V[i] - Vp)/Vmax;
			if (dif > err) {
				err = dif;
			}
		}
	}

	if (step >= maxStep) {
		cout << "Poisson's equation did not converge." << endl;
	} else {
		cout << "Poisson's equation converged." << endl;
	}
	cout << "step: " << step << endl;
	cout << "err:  " << err  << endl;

	return true;
}

ρ/ε部に関してはファンクタRhoOverEpsとして与えています．では実際にこのsolvePoisson1Dを使ってみましょう．なお，setVectorとmakeVectorはcalc.h（http://codepad.org/o7FsJVj3）で，CGnuplotはgnuplot.h，gnuplot.cpp（d:id:hecomi:20100714）を使用しています．

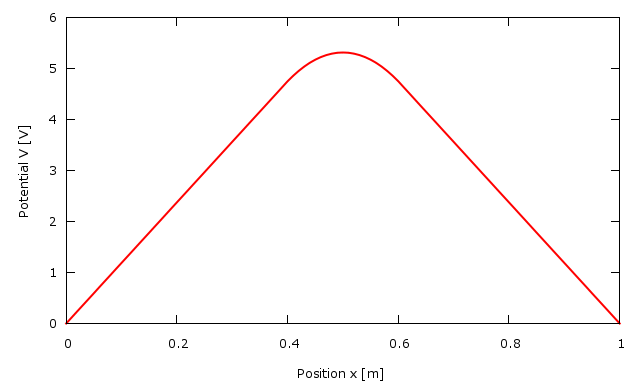
#include "calc.h"
#include "poisson.h"
#include "gnuplot.h"		// GNUPLOTを使用するためのクラス

using namespace calc;
using namespace std;

int main()
{
	// 物理定数
	const double eps = 8.85418782e-12;

	// 計算用ベクトル
	vector<double> x, V;
	
	// xベクトル作成（100分割）
	makeVector(x, 0.0, 1.0, 100);

	// Vベクトル初期値セット（全て0）
	setVector(V, x, 0*_1);

	// 電荷分布作成（0.4〜0.6に1e-9[Cm^-3]）
	boost::function<double(double)> roe = 
		if_then_else_return(bind(fabs, _1 - 0.5) < 0.1, 1e-9/eps, 0);

	// ポアソン方程式を解く
	solvePoisson1D(V, x, roe);

	// プロット
	CGnuplot gp;
	gp.SetLabel("Position x [m]", "Potential V [V]");
	gp.Plot(x, V);

	// 待ち
	int num;
	cin >> num;
}

結果：

考察

1次元ポアソン方程式では，電荷がある場合2次関数に，電荷がない場合1次関数となります．概ね良さそうですね．

凹みTips

C++、JavaScript、Unity、ガジェット等の Tips について雑多に書いています。

C++で1次元ポアソン方程式を解く

理論

プログラム

考察