C++で2次元ポアソン方程式を解く

前回のエントリ(d:id:hecomi:20100717:1279390033）では1次元のポアソン方程式を解いたので2次元を解いてみようと思います．理論は2次元になっただけでほぼ同じです．

使用プログラム

ベクトルセット等：

calc.h

3次元プロットに対応したCGnuplot：

2次元ポアソン方程式計算

poisson.h

#include <vector>
#include <iostream>
#include <cmath>
#include <boost/multi_array.hpp>

/*
@brief 2次元ポアソン方程式をSOR法により計算する（ディリクレ条件）
@param[out] V 対称のポテンシャルベクトル
@param[in]  x 対応する位置のベクトル
@param[in]  y 対応する位置のベクトル
@param[in]  RhoOverEPS 電荷分布を表すファンクタ
@param[in]  minErr 収束最小値
@param[in]  maxStep 最大計算ループ数
@param[in]  w SOR法係数
*/
template <class Container, class Functor>
int solvePoisson2D(boost::multi_array<double, 2> &V, const Container &x, const Container &y, Functor RhoOverEps,
				   const double minErr = 1e-5, const double maxStep = 1000, const double w = 1.9)
{
	using namespace std;

	// vectorサイズ一致の確認
	const int divX = x.size();
	const int divY = y.size();
	const int divZ = V.shape()[0] * V.shape()[1];
	if (divZ != divX*divY) {
		cout << "V.size() != x.size()*y.size() @solvePoisson2D" << endl;
		return false;
	}

	// vector最小数
	if (divX < 3 || divY < 3) {
		cout << "x.size() or y.size() < 3 @solvePoisson2D" << endl;
		return false;
	}

	// 単調増加か
	for (int i=0; i<divX-1; i++) {
		if (x[i] > x[i+1]) {
			std::cout << "Error! x must be monotonically increasing. (@solvePoisson2D)" << std::endl;
			return false;
		}
	}
	for (int j=0; j<divX-1; j++) {
		if (y[j] > y[j+1]) {
			std::cout << "Error! y must be monotonically increasing. (@solvePoisson2D)" << std::endl;
			return false;
		}
	}

	// 微分幅を得る
	const double dx = x[1] - x[0];
	const double dy = y[1] - y[0];

	// 誤差初期値
	double err = 2*minErr;

	// ループ回数
	int step = 0;

	// 誤差が最小誤差よりも小さくなるか，maxStepに到達するまでセルフコンシステント計算
	double Vmax = 0.0;
	while (err > minErr && step++ < maxStep) {
		err = 0;
		// 差分法を適用
		for (int i=1; i < divX-1; i++) {
			for (int j=1; j < divY-1; j++) {
				double Vp = V[i][j];

				// Poisson方程式
				V[i][j] = Vp + w * (
					1/(2*(dx*dx + dy*dy)) * (
						(dx*dx*dy*dy) * RhoOverEps(x[i], y[j])
						+ dx*dx*(V[i][j-1] + V[i][j+1]) + dy*dy*(V[i-1][j] + V[i+1][j])
					) - V[i][j]
				);

				// 規格化用Vを計算
				if (fabs(V[i][j]) > Vmax) {
					Vmax = fabs(V[i][j]);
				}

				// 誤差計算
				double dif = abs(V[i][j] - Vp)/Vmax;
				if (dif > err) {
					err = dif;
				}
			}
		}
	}

	if (step >= maxStep) {
		cout << "Poisson's equation did not converge." << endl;
	} else {
		cout << "Poisson's equation converged." << endl;
	}
	cout << "step: " << step << endl;
	cout << "err:  " << err  << endl;

	return true;
}

main.cpp

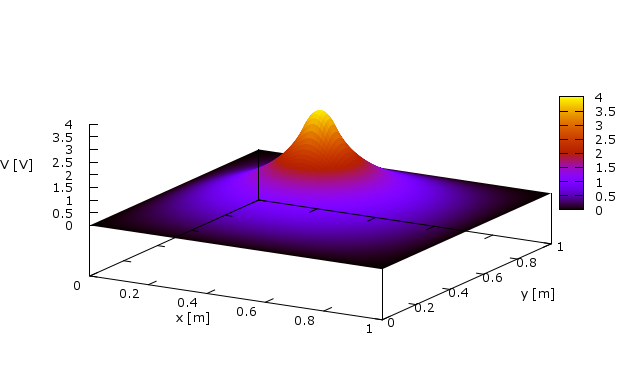
#define USE_BOOST // boostの使用（gnuplot.h）
#include "calc.h"
#include "poisson.h"
#include "gnuplot.h"

using namespace calc;
using namespace std;

int main()
{
	// 物理定数
	const double eps = 8.85418782e-12;

	// 分割数
	const int N = 100;

	// 計算用ベクトル
	vector<double> x, y;
	boost::multi_array<double, 2> V(boost::extents[N+1][N+1]);
	
	// x, yベクトル作成（0〜1[m]）
	makeVector(x, 0.0, 1.0, N);
	makeVector(y, 0.0, 1.0, N);

	// Vベクトル作成（境界条件はディリクレ，端は0 [V]）
	setVector(V, x, y, _1*0);

	// 電荷分布作成（中心に10[cm]幅）
	const double q = 1e-8;
	boost::function<double(double, double)> roe =
		if_then_else_return(
			bind(fabs, (_1-0.5)*(_1-0.5) + (_2-0.5)*(_2-0.5)) < 0.05*0.05,
			q/eps,
			0.0
		);

	// ポアソン方程式を解く
	solvePoisson2D(V, x, y, roe);

	CGnuplot gp;
	gp.Plot(x, y, V);
	gp.SetLabel("x [m]", "y [m]");
	gp.Command("set zlabel 'V [V]'");
	gp.Replot();
	gp.DumpToPng("poisson");

	// 待ち
	int num;
	cin >> num;
}